嘘つきパズルって…
皆さん知っての通り、「嘘つきパズル」とは、推理力を試される知的ゲームの一種です。そのパズルでは、複数の登場人物が登場し、そのうちの一部が嘘をついているという設定になっています。プレイヤーは彼らの発言の矛盾点や論理を分析し、誰が嘘をついているのか、またはどの情報が真実なのかを推理します。
今回は一風変わった嘘つきパズルをご紹介しようと思います。一見わかるわけがないと思うようなパズルですが、よくよくじっくり考えれば、聡明なあなたならきっと答えにたどり着けるはずです。
問題
郵便局長は、お友達である「謎解き君」に噓つきパズルを出題しようとしました。
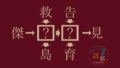
郵便局長が「謎解き君」に渡した問題の紙は以下の通りです。

なんということでしょう!
郵便局長が渡した問題は、もともと数字が書いてあった場所が汚れて見えなくなっているではありませんか!
郵便局長は「せっかく作ったのに…」と悲しみました。
謎解き君はこの紙を見て郵便局長に質問しました。
「この問題の答えは一つだけになるかい?」
郵便局長は「ああ、そうだよ。」と答えました。
謎解き君は言いました。
「じゃあ、もう答えはわかったよ。」
汚れで隠された部分に書かれていた数字はなんだったのでしょうか?
ただしそれぞれの人は、存在しない番号の人に対して言及することはありません。また、噓つきパズルでは、正直者は常に本当のことを言い、噓つきは常に噓をつきます。さらに、「私は嘘つきである。」という文章が噓つきパズルに含まれるとき、自己言及のパラドックスとなってしまうため、そのパズルは解答不能(つまり解無し)と見なされます。
ヒント1
数字が全然登場しないのに答えが分かるわけないだろ!
と言いたくなりますが、実は選択肢はそう多くありません。
注目すべきは「それぞれの人は、存在しない番号の人に対して言及することはない。」という点です。
つまりこの時点でA, Bはそれぞれ1, 2, 3のどれかを取るしかないのは確定するので、AとBの組み合わせは高々9通りです。
ヒント2
もう一つ注目すべきところは「嘘つきが一人だけ」という点です。
つまり「1番目の人が嘘つき」、「2番目の人が嘘つき」、「3番目の人が嘘つき」の3つの場合で場合分けすれば、隠された数字がいくつかによって、A, Bの組み合わせが何通りになるかわかります。
そして、A, Bの組み合わせが1つしか無いときこそ、まさに謎解き君が質問した「この問題の答えが一つだけになる。」状態そのものです!
解答・解説を見る
答えは5でした!
なぜそうなるのでしょうか?
まず、嘘つきが一人だけなので、「1番目の人が嘘つき」、「2番目の人が嘘つき」、「3番目の人が嘘つき」の3つの場合で場合分けをして考えます。ここで、汚れで隠された数字をNと置くことにします。
「2番目の人が嘘つき」の場合に注目してみましょう。2番目の人が嘘つきということは、1番目と3番目の人は正直者です。ということは ③「B番目の人は嘘つきさ。」のBには必ず2が入ります。一方、①「A番目の人は正直者だよ。」のAには1か3が入ります。したがって、AとBの組み合わせは(A, B)=(1, 2), (3, 2)の2種類が考えられます。
2番目の人は嘘つきという前提があるので、(A, B)=(1, 2)のとき、Nは3以外の全ての数を取る可能性があります。そして、(A, B)=(3, 2)のとき、Nは5以外の全ての数を取る可能性があります。つまり、「2番目の人が噓つき」という場合において、N=3のとき(A, B)=(3, 2)という1つの答えを取る可能性があります。N=5のとき(A, B)=(1, 2)という1つの答えを取る可能性があります。そしてそれ以外のとき、(A, B)=(1, 2), (3, 2)という2つの答えを取る可能性があります。ですが、謎解き君の質問によって、答えは一つだけになるということが分かっています。よってNが3か5以外の場合、答えが複数存在できてしまうため、そのような場合はありえないことがわかります。つまり、この時点でNは3か5以外ありえないのです!
「1番目の人が嘘つき」の場合に注目してみましょう。そのとき、 ①「A番目の人は正直者だよ。」のAには1だけが入ります。そうじゃないと1番目の人が嘘つきでなくなってしまいます。そして、3番目の人は正直者なので、③「B番目の人は嘘つきさ。」のBには必ず1が入ります。また、2番目の人も正直者なので②「AとBの合計は2になるね。」といったはずです。つまり、Nが2の場合は(A, B)=(1, 1)という答えを取る可能性があることがわかるのですが、そもそもNは3か5のどちらか以外ありえないので、この場合分けは特に答えを絞れません。
最後に、「3番目の人が嘘つき」の場合に注目してみましょう。このとき、1番目の人は正直者なので、 ①「A番目の人は正直者だよ。」のAには1か2が入ります。また、3番目の人は嘘つきなので、③「B番目の人は嘘つきさ。」のBには1か2が入ります。(Bに3を入れると自己言及のパラドックスになってしまうので答えになりません。)したがって、AとBの組み合わせは(A, B)=(1, 1), (1, 2), (2, 1), (2, 2)の4種類が考えられます。2番目の人は正直者なので、Nが2の場合は(A, B)=(1, 1)という答えを、Nが4の場合は(A, B)=(2, 2)という答えを、そしてNが3の場合は(A, B)=(1, 2)、(2, 1)という答えを取る可能性があることが分かります。よってNが3だったら、答えが一つだけになるということに矛盾してしまうので、消去法的に答えは5ということになります!
(大変でしたね…)




コメント